বীজগণিতীয় প্রতীক দ্বারা প্রকাশিত যেকোনো সাধারণ নিয়ম বা সিদ্ধান্তকে বীজগণিতীয় সূত্র বা সংক্ষেপে সূত্র বলা হয়। আমরা বিভিন্ন ক্ষেত্রে সূত্র ব্যবহার করে থাকি। এ অধ্যায়ে প্রথম চারটি সূত্র এবং এ চারটি সূত্রের সাহায্যে অনুসিদ্ধান্ত নির্ণয়ের পদ্ধতি দেখানো হয়েছে। এ ছাড়া বীজগণিতীয় সূত্র ও অনুসিদ্ধান্ত প্রয়োগ করে বীজগণিতীয় রাশির মান নির্ণয় ও উৎপাদকে বিশ্লেষণ উপস্থাপন করা হয়েছে। আবার বীজগণিতীয় রাশির সাহায্যে ভাজ্য, ভাজক, গুণনীয়ক, গুণিতক সম্পর্কে ধারণা দেওয়া হয়েছে এবং কীভাবে অনূর্ধ্ব তিনটি বীজগণিতীয় রাশির গ.সা.গু. ও ল.সা.গু. নির্ণয় করা যায় তা আলোচনা করা হয়েছে।

অধ্যায় শেষে শিক্ষার্থীরা -

• বর্গ নির্ণয়ে বীজগণিতীয় সূত্রের বর্ণনা ও প্রয়োগ করতে পারবে।
• বীজগণিতীয় সূত্র ও অনুসিদ্ধান্ত প্রয়োগ করে রাশির মান নির্ণয় করতে পারবে।
• বীজগণিতীয় সূত্র প্রয়োগ করে উৎপাদকে বিশ্লেষণ করতে পারবে।
• গুণনীয়ক ও গুণিতক কী তা ব্যাখ্যা করতে পারবে।
• অনূর্ধ্ব তিনটি বীজগণিতীয় রাশির সাংখ্যিক সহগসহ গ.সা.গু. ও ল.সা.গু. নির্ণয় করতে পারবে ।

সূত্র ১। $(a+b{)}^2=a^2+2ab+b^2$

প্রমাণ:

$(a+b{)}^2$ এর অর্থ (a + b) কে (a + b) দ্বারা গুণ।

$(a+b{)}^2=(a+b\left)\right(a+b)$

= a(a + b) + b(a + b) [বহুপদী রাশিকে বহুপদী রাশি দ্বারা গুণ]

$=a^2+ab+ba+b^2$

$=a^2+ab+ab+b^2$

$(a+b{)}^2=a^2+2ab+b^2$

সূত্রটির জ্যামিতিক ব্যাখ্যা

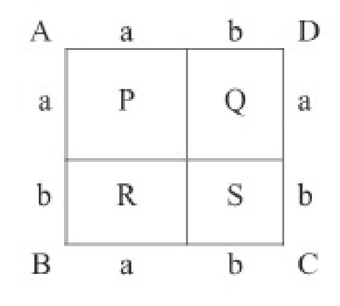
ABCD একটি বর্গক্ষেত্র যার

AB বাহু = a + b
BC বাহু = a+b

ABCD বর্গক্ষেত্রের ক্ষেত্রফল = (বাহুর দৈর্ঘ্য)^২

= (a + b)^২

বর্গক্ষেত্রটিকে P.Q, R, S চারটি ভাগে ভাগ করা হয়েছে।

এখানে P ও S বর্গক্ষেত্র এবং Q ও R আয়তক্ষেত্র।

আমরা জানি, বর্গক্ষেত্রের ক্ষেত্রফল = (দৈর্ঘ্য)² এবং আয়তক্ষেত্রের ক্ষেত্রফল = দৈর্ঘ্য $\times$ প্রস্থ

অতএব,

P এর ক্ষেত্রফল = $a\times a=a^2$

Q এর ক্ষেত্রফল = $a\times b = ab$

R এর ক্ষেত্রফল = $a\times b = ab$

S এর ক্ষেত্রফল = $b\times b=b^2$

এখন, ABCD বর্গক্ষেত্রের ক্ষেত্রফল = (P+Q+R+S) এর ক্ষেত্রফল

$(a+b{)}^2=a^2+ab+ab+b^2$

$=a^2+2ab+b^2$

$\therefore$ $(a+b{)}^2=a^2+2ab+b^2$

অনুসিদ্ধান্ত ১। $a^2+b^2=(a+b{)}^2-2ab$

আমরা জানি, $(a+b{)}^2=a^2+2ab+b^2$

বা, $(a+b{)}^2-2ab=a^2+2ab+b^2-2ab$ [উভয়পক্ষ থেকে 2ab বিয়োগ করে]

বা, $(a+b{)}^2-2ab=a^2+b^2$

$\therefore$ $a^2+b^2=(a+b{)}^2-2ab$

উদাহরণ ১। (m + n) এর বর্গ নির্ণয় কর।

সমাধান:

(m + n) এর বর্গ = $(m+n{)}^2$

$=(m{)}^2+2mn+(n{)}^2$

$=m^2+2mn+n^2$

উদাহরণ ২। (3x + 4) এর বর্গ নির্ণয় কর।

সমাধান:

(3x + 4) এর বর্গ = $(3x+4{)}^2$

$=(3x{)}^2+2\times 3x\times 4+(4{)}^2$

$=9x^2+24x+16$

উদাহরণ ৩। (2x + 3y) এর বর্গ নির্ণয় কর।

সমাধান:

(2x + 3y) এর বর্গ = $(2x+3y{)}^2$

$=(2x{)}^2+2\times 2x\times 3y+(3y{)}^2$

$=4x^2+12xy+9y^2$

উদাহরণ ৪। বর্গের সূত্র প্রয়োগ করে 105 এর বর্গ নির্ণয় কর।

সমাধান:

$(105{)}^2=(100+5{)}^2$

$=(100{)}^2+2\times 100\times 5+(5{)}^2$

= 10000+1000+25

= 11025

সূত্র ২। $(a-b{)}^2=a^2-2ab+b^2$

${(a-b)}^2$ এর অর্থ (a-b) কে (a-b) দ্বারা গুণ।

$\therefore$ $(a-b{)}^2=(a-b\left)\right(a-b)$

=a(a-b)-b(a-b)

$= a^2-ab-ba + b^2$

$= a^2-ab-ab+b^2$

$\therefore$ $(a-b{)}^2=a^2-2ab+b^2$

লক্ষ করি: দ্বিতীয় সূত্রটি প্রথম সূত্রের সাহায্যেও নির্ণয় করা যায়।

আমরা জানি,

$(a+b{)}^2=a^2+2ab+b^2$

এখন

$(a-b{)}^2= (a+(-b){ }^2=a^2+2a(-b)+(-b{)}^2$ [b এর পরিবর্তে - b বসিয়ে ]

$=a^2-2ab+b^2$

অনুসিদ্ধান্ত ২। $a^2+b^2=(a-b{)}^2+2ab$

আমরা জানি, $(a-b{)}^2=a^2-2ab+b^2$

বা, $(a-b{)}^2+2ab=a^2-2ab+b^2+2ab$

বা, $(a-b{)}^2+2ab=a^2+b^2$

$\therefore$ $a^2+b^2=(a-b{)}^2+2ab$

উদাহরণ ৫। p - q এর বর্গ নির্ণয় কর।

সমাধান:

(p + q) এর বর্গ = $(p-q{)}^2$

$=(p{)}^2-2pq+(q{)}^2$

$=p^2-2pq+q^2$

উদাহরণ ৬। (5x - 3y) এর বর্গ নির্ণয় কর।

সমাধান:

(5x + 3y) এর বর্গ = $(5x-3y{)}^2$

$=(5x{)}^2-2\times 5x\times 3y+(3y{)}^2$

$=25x^2-30xy+9y^2$

উদাহরণ ৭। বর্গের সূত্র প্রয়োগ করে 98 এর বর্গ নির্ণয় কর।

সমাধান:

$(98{)}^2=(100-2{)}^2$

$=(100{)}^2-2\times 100\times 2+(2{)}^2$

=10000-400+4

= 9604

প্রথম ও দ্বিতীয় সুত্রের আরও কয়েকটি অনুসিদ্ধান্ত:

অনুসিদ্ধান্ত ৩।

$(a+b{)}^2=a^2+2ab+b^2$

$=a^2+b^2-2ab+4ab$ $[ \because + 2ab = - 2ab + 4ab ]$

$=a^2-2ab+b^2+4ab$

$=(a-b{)}^2+4ab$

$\therefore$ $(a+b{)}^2=(a-b{)}^2+4ab$

অনুসিদ্ধান্ত ৪।

$(a-b{)}^2=a^2-2ab+b^2$

$=a^2+b^2+2ab-4ab$

$=a^2+2ab+b^2-4ab$

$=(a-b{)}^2-4ab$

$\therefore$$(a-b{)}^2=(a+b{)}^2-4ab$

অনুসিদ্ধান্ত ৫।

$(a+b{)}^2+(a-b{)}^2=(a^2+2ab+b^2)+(a^2-2ab+b^2)$

$=a^2+2ab+b^2+a^2-2ab+b^2$

$=2a^2+2b^2$

$=2(a^2+b^2)$

$\therefore$$(a+b{)}^2+(a-b{)}^2=2(a^2+b^2)$

অনুসিদ্ধান্ত ৬।

$(a+b{)}^2-(a-b{)}^2=(a^2+2ab+b^2)-(a^2-2ab+b^2)$

$=a^2+2ab+b^2-a^2+2ab-b^2$

= 4ab

$\therefore$ $(a+b{)}^2-(a-b{)}^2=4ab$

উদাহরণ ৮। a + b = 7 এবং ab = 9 হলে, a² + b² এর মান নির্ণয় কর।

সমাধান:

আমরা জানি,

$a^2+b^2=(a+b{)}^2-2ab$

$= {\left(7\right)}^2-2x9$

=49-18

=31

উদাহরণ ৯। a + b = 5 এবং ab = 6 হলে, (a-b)² এর মান নির্ণয় কর।

সমাধান:

আমরা জানি,

$(a-b{)}^2=(a+b{)}^2-4ab$

$= {\left(5\right)}^2-4x6$

=25-24

=1

উদাহরণ ১০। $p-\frac{1}{p}=8$ হলে, প্রমাণ কর যে $p^2+\frac{1}{p^2}=66$

সমাধান:

$p^2+\frac{1}{p^2}= {\left(p-\frac{1}{p}\right)}^2+2\times p\times \frac{1}{p}$ $[\because a^2+b^2=(a-b{)}^2+2ab]$

$=(8{)}^2+2$

= 64+2

= 66 (প্রমাণিত)

উদাহরণ ১১। a + b + c এর বর্গ নির্ণয় কর।

সমাধান:

ধরি, a + b = p

$\therefore$ $(a+b+c{)}^2$

$=\left\{\right(a+b)+c{\}}^2$

$=(p+c{)}^2$

$=p^2+2pc+c^2$

$=(a+b{)}^2+2(a+b)c+c^2$

$=a^2+2ab+b^2+2ac+2bc+c^2$

$=a^2+b^2+c^2+2ab+2bc+2ca$

উদাহরণ ১২। (x + y - z) এর বর্গ নির্ণয় কর।

সমাধান:

ধরি, x + y = m

$\therefore (x+y-z{)}^2= \left\{x+y)-z{ }^2\right\}$

$=(m-z{)}^2$

$=m^2-2mz+z^2$

$=(x+y{)}^2-2x(x+y)z+z^2$ [m-এর মান বসিয়ে]

$=x^2+2xy+y^2-2xz-2yz+z^2$

$=x^2+y^2+z^2+2xy-2xz-2yz$

উদাহরণ ১৩। 3x - 2y + 5z এর বর্গ নির্ণয় কর।

সমাধান:

3x - 2y + 5z এর বর্গ

$=\left\{\right(3x-2y)+5z{\}}^2$

$=(3x-2y{)}^2+2(3x-2y)5z+(5z{)}^2$

$=(3x{)}^2-2\times 3x\times 2y+(2y{)}^2+2\times 5z(3x-2y)+25z^2$

$=9x^2-12xy+4y^2+30xz-20yz+25z^2$

$=9x^2+4y^2+25z^2-12xy+30xz-20yz$

উদাহরণ ১৪। সরল কর: $(2x+3y{)}^2-2(2x+3y\left)\right(2x-5y)+(2x-5y{)}^2$

সমাধান:

ধরি, 2x + 3y = a এবং 2x - 5y = b

প্রদত্ত রাশি

$=a^2-2ab+b^2$

$=\left\{\right(2x+3y)-(2x-5y){\}}^2$

$=\{2x+3y-2x+5y{\}}^2$

$= {\left(8y\right)}^2$

$= 64y^2$

উদাহরণ ১৫। x = 7 এবং y = 6 হলে, $16x^2-40xy+25y^2$ এর মান নির্ণয় কর।

সমাধান: প্রদত্ত রাশি

$= 16x^2-40xy+25y^2$

$=(4x{)}^2-2\times 4x\times 5y+(5y{)}^2$

$={(4x-5y)}^2$

$={(4x7-5x6)}^2$

$= {(28-30)}^2$

$= {(-2)}^2$

$= (- 2)(- 2)$

= 4

সূত্রের সাহায্যে বর্গ নির্ণয় কর (১-১৬)।

১| a + 5

২। 5x - 7

৩। 3a-11xy

৪। $5a^2+9m^2$

৫ |55

৬।990

৭। xy - 6y

৮। ax - by

৯। 97

১০। x + y - z

১১। 2a - b + 3c

$১২। x^2+y^2-z^2$

১৩। a - 2b - c

১৪ । 3x -2y + z

১৫| bc + ca + ab

$১৬।2a^2+2b-c^2$

সরল কর (১৭-২৪)।

$১৭। (2a+1{)}^2-4a(2a+1)+4a^2$

$১৮।(5a+3b{)}^2+2(5a+3b\left)\right(4a-3b)+(4a-3b{)}^2$

$১৯।(7a+b{)}^2-2(7a+b\left)\right(7a-b)+(7a-b{)}^2$

$২০।(2x+3y{)}^2+2(2x+3y\left)\right(2x-3y)+(2x-3y{)}^2$

$২১।(5x-2{)}^2+(5x+7{)}^2-2(5x-2)(5x+7)$

$২২।(3ab-cd{)}^2+9(cd-ab{)}^2+6(3ab-cd)(cd-ab)$

$২৩।(2x+5y+3z{)}^2+(5y+3z-x{)}^2-2(5y+3z-x)(2x+5y+3z)$

$২৪।(2a-3b+4c{)}^2+(2a+3b-4c{)}^2+2(2a-3b+4c)(2a+3b-4c)$

মান নির্ণয় কর (২৫-২৮):

$২৫।25x^2+36y^2-60xy যখন x=-4y=-5$

$২৬।16a^2-24ab+9b^2 যখন a=7b=6$

$২৭। 9x^2+30x+25 যখন x=-2$

$২৮। 81a^2+18ac+c^2 যখন a=7,c=-67$

২৯। a - b = 7 এবং ab = 3 হলে, দেখাও যে, $(a+b{)}^2=61$

৩০। a + b = 5 এবং ab = 12 হলে, দেখাও যে, $a^2+b^2=1$

৩১। $x+\frac{1}{x}=5$ হলে, প্রমাণ কর যে, $\left(x^2-\frac{1}{x^2}\right)=525$

৩২। a + b = 8 এবং a - b = 4 হলে, ab = কত?

৩৩। x + y = 7 এবং xy = 10 হলে, $x^2+y^2+5xy$ এর মান কত?

সূত্র ৩। $(a+b)(a-b)=a^2-b^2$

প্রমাণ:

$(a + b)(a - b) = a(a - b) + b(a - b)$

$=a^2-ab+ab-b^2$

$\therefore$ $(a+b)(a-b)=a^2-b^2$

উদাহরণ ১৬। সূত্রের সাহায্যে 3x + 2y কে 3x - 2y দ্বারা গুণ কর।

সমাধান:

(3x + 2y)(3x - 2y)

$=(3x{)}^2-(2y{)}^2$

$=9x^2-4y^2$

উদাহরণ ১৭। সূত্রের সাহায্যে $a{x}^2 + b$ কে $a{x}^2-b$ দ্বারা গুণ কর।

সমাধান:

$(a{x}^2+b)(a{x}^2-b)$

$= {\left(a{x}^2\right)}^2-{\left(b\right)}^2$

$= a^2{x}^4-b^2$

উদাহরণ ১৮। সূত্রের সাহায্যে 3x + 2y + 1 কে 3x - 2y + 1 দ্বারা গুণ কর।

সমাধান:

(3x + 2y + 1)(3x - 2y + 1)

= {(3x + 1) + 2y}{(3x + 1) - 2y}

$=(3x+1{)}^2-(2y{)}^2$

$=9x^2+6x+1-4y^2$

$=9x^2-4y^2+6x+1$

সূত্র ৪। $(x+a)(x+b)=x^2+(a+b) x+ab$

প্রমাণ:

$(x + a)(x + b) = (x + a) x + (x + a) b$

$=x^2+ax+bx+ab$

$=x^2+(a+b)x+ab$

অর্থাৎ, $(x+a)(x+b)=x^2+$ (a এবং b এর বীজগণিতীয় যোগফল) x +(a এবং b এর গুণফল)

উদাহরণ ১৯। a + 3 কে a + 2 দ্বারা গুণ কর।

সমাধান:

(a + 3)(a + 2)

$=a^2+(3+2)a+3\times 2$

$=a^2+5a+6$

উদাহরণ ২০। px + 3 কে px - 5 দ্বারা গুণ কর।

সমাধান:

(px + 3)(px - 5)

$=(px{)}^2+\{3+(-5)\} px+3(-5)$

$=p^2{x}^2+(3-5)px-15$

$=p^2{x}^2+(-2) px-15$

$=p^2{x}^2-2px-15$

সূত্রের সাহায্যে গুণফল নির্ণয় কর:

১। (4x + 3) , (4x - 3)

২। (13 - 12p) , (13 + 12p)

৩। (ab + 3) , (ab - 3)

8 (10 - xy) , (10 + xy)

$৫। (4x^2+3y^2) , (4x^2-3y^2)$

৬। (a - b - c) , (a + b + c)

$৭। (x^2-x+1) , (x^2+x+1)$

$৮। (a^4+3a^2 x^2+9x^4),(9x^4-3a^2 x^2+a^4)$

$৯। (x+1)(x-1)(x^2+1)$

$১০। (9a^2+b^2)(3a+b),(3a-b)$

আমরা জানি, $6 = 2 \times 3$

এখানে, 2 ও 3 হলো 6 এর দুইটি উৎপাদক বা গুণনীয়ক।

৩ নং সূত্র থেকে আমরা জানি, $a^2-b^2=(a+b)(a-b)$

তাহলে, (a + b) ও (a - b) বীজগণিতীয় রাশি $a^2-b^2$ এর দুটি উৎপাদক বা গুণনীয়ক।

বীজগণিতীয় বিভিন্ন সূত্র এবং গুণের বিনিময়বিধি, সংযোগবিধি ও বণ্টনবিধি ব্যবহার করে বীজগণিতীয় রাশিকে উৎপাদকে বিশ্লেষণ করা হয়।

গুণনের বণ্টনবিধির সাহায্যে উৎপাদকে বিশ্লেষণ

উদাহরণ ২২। 20x +4y কে উৎপাদকে বিশ্লেষণ কর।

সমাধান:

$20x + 4y = 4 \times 5x + 4y$

= 4(5x + y) [গুণের বণ্টনবিধি অনুযায়ী]

উদাহরণ ২৩। ax-by+ax by কে উৎপাদকে বিশ্লেষণ কর।

সমাধান:

ax - by + ax - by

= ax + ax-by-by

= 2ax - 2by [গুণের বণ্টনবিধি অনুযায়ী]

= 2(ax-by)

উদাহরণ ২৪। উৎপাদকে বিশ্লেষণ কর: $2x-6x^2$

সমাধান: $2x-6x^2=2x(1-3x)$

উদাহরণ ২৫। উৎপাদকে বিশ্লেষণ কর: $x^2+4x+xy+4y$

সমাধান:

$x^2+4x+xy+4y$

$= x(x + 4) + y(x + 4)$

= (x + 4)(x + y)

লক্ষ করি: দুটি রাশি এমনভাবে নির্বাচন করতে হবে যেন বণ্টনবিধি প্রয়োগ করে প্রাপ্ত রাশি দুটির মধ্যে একটি সাধারণ উৎপাদক পাওয়া যায়।

বীজগণিতীয় সূত্রের সাহায্যে উৎপাদকে বিশ্লেষণ

উদাহরণ ২৬। উৎপাদকে বিশ্লেষণ কর: $25-9x^2$

সমাধান: $25-9x^2=(5{)}^2-(3x{)}^2=(5+3x)(5-3x)$

উদাহরণ ২৭। $8x^4-2x^2{a}^2$ কে উৎপাদকে বিশ্লেষণ কর।

সমাধান: $8x^4-2x^2{a}^2=2x^2(4x^2-a^2)$ [বণ্টনবিধি অনুযায়ী]

$=2x^2\left\{\right(2x{)}^2-\left(a{)}^2\right\}=2x^2(2x+a)(2x-a)$

উদাহরণ ২৮। উৎপাদকে বিশ্লেষণ কর: $25(a+2b{)}^2-36(2a-5b{)}^2$

সমাধান: ধরি, a + 2b = x এবং 2a - 5b = y

প্রদত্ত রাশি

$=25x^2-36y^2$

$= {\left(5x\right)}^2- {\left(6y\right)}^2$

$= (5x+6y)(5x-6y)$

$=5(a+2b)+6(2a-5b)5(a+2b)-6(2a-5b)$ [x ও y এর মান বসিয়ে]

$=(5a+10b+12a-30b)(5a+10b-12a+30b)$

$=(17a-20b)(40b-7a)$

উদাহরণ ২৯। উৎপাদকে বিশ্লেষণ কর: $4x^2-4xy+y^2-z^2$

সমাধান:

$4x^2-4xy+y^2-z^2$

$=(2x{)}^2-2\times 2x\times y+(y{)}^2-z^2$

$=(2x-y{)}^2-(z{)}^2$

$= (2x - y + z)(2x - y - z)$

উদাহরণ ৩০। উৎপাদকে বিশ্লেষণ কর: $2bd-a^2-c^2+b^2+d^2+2ac$

সমাধান:

$2bd-a^2-c^2+b^2+d^2+2ac$

$=b^2+2bd+d^2-a^2+2ac-c^2$ [সাজিয়ে]

$=(b^2+2bd+d^2)-(a^2-2ac+c^2)$

$=(b+d{)}^2-(a-c{)}^2$

= (b + d + a - c)(b + d - a + c)

= (a + b - c + d)(b - a + c + d)

উৎপাদকে বিশ্লেষণ কর।

$১। x^2+xy+zx+yz$

$২। a^2+bc+ca+ab$

$৩। ab(px+qy)+a^{2}qx+b^{2}py$

$8। 4x^2-y^2$

$৫। 9a^2-4b^2$

$৬। a^2{b}^2-49y^2$

$৭। 16x^4-81y^4$

$৮। a^2-(x+y{)}^2$

$৯। (2x-3y+5z{)}^2-(x-2y+3z{)}^2$

$১০। 4+8a^2+9a^4$

$১১। 2a^2+6a-80$

$১২। y^2-6y-91$

$১৩। p^2-15p+56$

$১৪। 45a^8-5a^4{x}^4$

$১৫। a^2+3a-40$

$১৬। (x^2+1{)}^2-(y^2+1{)}^2$

$১৭। x^2+11x+30$

$১৮। a^2-b^2+2bc-c^2$

$১৯। 144x^7-25x^3{a}^4$

$২০। 4x^2+12xy+9y^2-16a^2$

x, y ও z তিনটি রাশি। ধরি,

এখানে একটি ভাগ প্রক্রিয়া দেখানো হয়েছে। x কে ভাগ করা হয়েছে, তাই x ভাজ্য। আবার, y দ্বারা ভাগ করা হয়েছে, ফলে y ভাজক এবং এ হলো ভাগফল।

যেমন, 10$÷$2 = 5

এখানে,

10 $\to$ ভাজ্য

2 $\to$ ভাজক

5$\to$ভাগফল

এক্ষেত্রে 10,2 এর একটি গুণিতক। আবার 10,5 এরও একটি গুণিতক। অপরদিকে 2 এবং 5 উভয় 10 এর উৎপাদক।

পাটিগণিত থেকে আমরা জেনেছি

12,18 ও 24 এর সাধারণ গুণনীয়কগুলো 2,3ও6। এদের মধ্যে বড় গুণনীয়কটি 6।

$\therefore$ 12,183 24 এর গ.সা.গু. 6

বীজগণিতে

xyz এর গুণনীয়কগুলো যথাক্রমে $\overline{)x},y,z$

5x এর গুণনীয়কগুলো যথাক্রমে $5, \overline{)x}$

3.xp এর গুণনীয়কগুলো যথাক্রমে $3, \overline{)x}, p$

$\therefore$x y z, 5x, 3xp রাশিগুলোর সাধারণ গুণনীয়ক x

$\therefore$রাশিগুলোর গ.সা.গু. x

গ.সা.গু. নির্ণয়ের নিয়ম

• পাটিগণিতের নিয়মে প্রদত্ত রাশিগুলোর সাংখ্যিক সহগের গ.সা.গু. নির্ণয় করতে হয়।
• বীজগণিতীয় রাশিগুলোর মৌলিক উৎপাদক বের করতে হয়।
• সাংখ্যিক সহগের গ.সা.গু. এবং প্রদত্ত রাশিগুলোর বীজগণিতীয় সাধারণ মৌলিক উৎপাদকগুলোর ধারাবাহিক গুণফল হচ্ছে নির্ণেয় গ.সা.গু.।

উদাহরণ ৩২। $৪x^{2}y{z}^2$ এবং $10x^3 y^2{z}^3$ এর গ.সা.গু. নির্ণয় কর।

সমাধান: $8x^{2}y{z}^2=2\times 2\times 2\times x\times x\times y\times z\times z$

$10x^3{y}^2{z}^3=2\times 5\times x\times x\times x\times y\times y\times z\times z\times z$

সুতরাং, দেখা যাচ্ছে সাধারণ গুণনীয়কগুলো 2, x, x, y, z, z.

নির্ণেয় গ.সা.গু. $2\times x\times x\times y\times z\times z=2x^{2}y{z}^2$

উদাহরণ ৩৩। $2(a^2-b^2)$ এবং $(a^2-2ab+b^2)$ এর গ.সা.গু. নির্ণয় কর।

সমাধান:

১ম রাশি = $2(a^2-b^2)=2(a+b)(a-b)$

২য় রাশি = $a^2-2ab+b^2=(a-b)(a-b)$

এখানে সাংখ্যিক সহগ 2 ও1 এর গ.সা.গু. = 1.

এবং সাধারণ মৌলিক উৎপাদক বা গুণনীয়ক (a-b)

নির্ণেয় গ.সা.গু. 1 × (a - b)

=(a-b)

উদাহরণ ৩৪। $x^2-4, 2x+4$ এবং $x^2+5x+6$ এর গ.সা.গু. নির্ণয় কর।

সমাধান:

১ম রাশি =$x^2-4=(x+2)(x-2)$

২য় রাশি = $2x + 4 = 2(x + 2)$

৩য় রাশি =$x^2+5x+6=x^2+2x+3x+6$

$= x(x + 2) + 3(x + 2) = (x + 2)(x + 3)$

এখানে প্রদত্ত রাশিগুলোর সাংখ্যিক সহগ 1, 2 এবং 1 এর গ.সা.গু. = 1

সাধারণ মৌলিক উৎপাদক = (x + 2)

নির্ণেয় গ.সা.গু. $1 \times (x + 2) = (x + 2)$

পাটিগণিতে আমরা জানি,

4 এর গুণিতকগুলো হচ্ছে 4,8,12,16, 20, 24, 28, 32, 36, _____________

6 “ ” " 6, 12, 18, 24, 30, 36, _____________

4 এবং 6 এর সাধারণ গুণিতক হচ্ছে 12, 24, 36 _____________

4 এবং 6 এর লঘিষ্ঠ সাধারণ গুণিতক হচ্ছে 12.

বীজগণিতীয় রাশির ক্ষেত্রে,

$x^2{y}^2÷\left(x^2\right)y=y$

এবং $x^2{y}^2÷x{y}^2=x$

অর্থাৎ $x^{2}y$ ও $x{y}^2$ এর প্রত্যেকটি দ্বারা $x^2{y}^2$ নিঃশেষে বিভাজ্য।

সুতরাং $x^2{y}^2$ হলো $x^{2}y \hspace{0.17em}ও x{y}^2$ এর একটি সাধারণ গুণিতক।

আবার, $x^{2}y=x\times x\times y$

$x{y}^2=x\times y\times y$

এখানে রাশি দুটিতে x আছে সর্বোচ্চ দুইবার এবং y আছে সর্বোচ্চ দুইবার।

ল.সা.গু. $=x\times x\times y\times y=x^2{y}^2$

মন্তব্য: ল.সা.গু. সাধারণ উৎপাদক $\times$ সাধারণ নয় এরূপ উৎপাদক।

ল.সা.গু. নির্ণয়ের নিয়ম

ল.সা.গু. নির্ণয় করার জন্য প্রথমে সাংখ্যিক সহগগুলোর ল.সা.গু. বের করতে হবে। এরপর উৎপাদকের সর্বোচ্চ ঘাত বের করতে হবে। অতঃপর উভয়ের গুণফলই হবে প্রদত্ত রাশিগুলোর ল.সা.গু.।

উদাহরণ ৩৫। $4x^2{y}^{3}z, 6.x{y}^3{z}^2$ এবং $৪x^2 y{z}^3$ এর ল.সা.গু. নির্ণয় কর।

সমাধান:

রাশিগুলোর সাংখ্যিক সহগ 4, 6ও৪ এর ল.সা.গু. 24 প্রদত্ত রাশিগুলোর অন্তর্ভুক্ত সর্বোচ্চ ঘাতবিশিষ্ট উৎপাদকগুলো যথাক্রমে $x^3, y^3 ও z^3$ নির্ণেয় ল.সা.গু. $24x^3{y}^3{z}^3$

উদাহরণ ৩৬। $a^2-b^2 ও\hspace{0.17em}{a}^2+2ab+b^2$ এর ল.সা.গু. নির্ণয় কর।

সমাধান:

১ম রাশি = $a^2-b^2=(a+b)(a-b)$

২য় রাশি = $a^2+2ab+b^2=(a+b{)}^2$

প্রদত্ত রাশিগুলোর সম্ভাব্য সর্বোচ্চ ঘাতবিশিষ্ট উৎপাদকগুলো $(a-b) ও\hspace{0.17em}(a+b{)}^2$

নির্ণেয় ল.সা.গু. $(a-b) (a+b{)}^2$

উদাহরণ ৩৭। $2x^{2}y+4x{y}^2,4x^{3}y-16x{y}^3$ এবং $5x^2{y}^2(x^2+4xy+4y^2)$ এর ল.সা.গু. নির্ণয় কর।

সমাধান:

১ম রাশি =$2x^{2}y+4x{y}^2=2xy(x+2y)$

২য় রাশি = $4x^{3}y-16x{y}^3=4xy(x^2-4y^2)=4xy(x+2y)(x-2y)$

৩য় রাশি = $5x^2{y}^2(x^2+4xy+4y^2)=5x^2{y}^2(x+2y{)}^2$

সাংখ্যিক সহগ 2, 435 এর ল.সা.গু. 20]

প্রদত্ত রাশিগুলোতে সম্ভাব্য সর্বোচ্চ ঘাতবিশিষ্ট উৎপাদকগুলো$x^2,y^2,(x+2y{)}^2,(x-2y)$

নির্ণেয় ল.সা.গু. $\left(20x^2{y}^2\right(x-2y\left)\right(x+2y{)}^2$

১। a - 5 এর বর্গ কোনটি?

$$\begin{gathered} \left(ক\right)a^2+10a+25 \\ \left(খ\right)a^2-10a+25 \\ (গ)a^2+5a+25 \\ (ঘ)a^2-5a+25 \end{gathered}$$

$২। (x+y{)}^2+2(x+y\left)\right(x-y)+(x-y{)}^2$ এর মান কোনটি?

$$\begin{gathered} \left(ক\right)8x^2 \\ \left(খ\right)8y^2 \\ \left(গ\right)4x^2 \\ \left(ঘ\right)4y^2 \end{gathered}$$

৩। a + b = 4 এবং a - b = 2 হলে, ab এর মান কত?

(ক) 3
(খ) ৪
(গ) 12
(ঘ) 16

81 একটি রাশি অপর একটি রাশি দ্বারা নিঃশেষে বিভাজ্য হলে, ভাজ্যকে ভাজকের কী বলা হয়?

(ক) ভাগফল
(খ) ভাগশেষ
(গ) গুণিতক
(ঘ) গুণনীয়ক

$৫। a,a^2,a(a+b)$ এর লঘিষ্ঠ সাধারণ গুণিতক কোনটি?

(ক) a
$\left(খ\right)a^2$
(গ) a(a + b)
$\left(ঘ\right)a^2(a+b)$

৬। 2a ও 3b এর গ.সা.গু. কত?

(ক) 1
(খ) 6
(গ) ab
(ঘ) 6ab

a, b বাস্তব সংখ্যা হলে-

$$\begin{gathered} ৭। \\ \left(i\right)(a+b{)}^2=a^2+2ab+b^2 \\ (ii)4ab=(a+b{)}^2+(a-b{)}^2 \end{gathered}$$
$\left(iii\right)a^2-b^2=(a+b)(a-b)$

কোনটি সঠিক?

(ক) i ও ii
(খ) i ও iii
(গ) ii ও iii
(ঘ) i, ii ও iii

$(x^{3}y-x{y}^3)ও (x-y)(x+2y)$ দুইটি বীজগণিতীয় রাশি।

উপরের তথ্যের আলোকে ৮-১০নং প্রশ্নের উত্তর দাও।

৮। প্রথম রাশির উৎপাদকে বিশ্লেষিত রূপ নিচের কোনটি?

(ক) (x + y)(x - y)
(খ) x(x + y)(x - y)
(গ) y(x + y)(x - y)
(ঘ) xy(x + y)(x - y)

৯। বীজগণিতীয় রাশি দুটির গ.সা.গু. নিচের কোনটি?

(ক) (x + y)
(খ) (x - y)
(গ) y(x + y)
(ঘ) x(x - y)

১০। বীজগণিতীয় রাশি দুটির ল.সা.গু. নিচের কোনটি?

(ক) x(x + y)(x - y)
(খ) y(x + y)(x-y)
(গ) $xy(x^2-y^2)(x+2y)$
(ঘ) xy(x + y)(x + 2y)

$১১। 9x^2-25y^2$ এবং 15ax-25ay এর ল.সা.গু কত?

(ক) (3x + 5y)
(খ) (3x-5)
$$\begin{gathered} \left(গ\right) (9x^2-25y^2) \\ \left(ঘ\right) 5a (9x^2-25y^2) \end{gathered}$$

$১২। x{y}^2 ও a^2-b^2$ এর গ.সা.গু কত?

(ক) x³y⁵
(খ) x²a²
(গ) xy⁴
(ঘ) 1

১৩। $x - \frac{1}{x}= 0$ হলে

(1) x = 1
(ii) x = - 1
(iii) x = $\pm$ 1

নিচের কোনটি সঠিক?

(ক) i ও ii
(খ) ii ও iii
(গ) i ও iii
(ঘ) i, ii ও iii

১৪। a + 5 এর বর্গ কোনটি?

$$\begin{gathered} \left(ক\right)a^2+10a+25 \\ \left(খ\right)a^2-10a+25 \\ \left(গ\right)a^2+5a+25 \\ \left(ঘ\right)a^2+5a-25 \end{gathered}$$

১৬। a + b = 8, a - b = 4 হলে ab = কতো ?

(ক) ৪
(খ) 10
(গ) 12
(ঘ) 18

গ.সা.গু. নির্ণয় কর (১৭-২৬)।

$১৭।3a^3{b}^{2}c , 6a{b}^2{c}^2$

$১৮। 5a{b}^2{x}^2 , 10a^{2}b{y}^2$

$১৯।3a^2{x}^2 , 6ax{y}^{2}9a{y}^2$

$২০। 16a^3{x}^{4}y , 40a^2{y}^{3}x28a{x}^3$

$২১। a^2+ab , a^2-b^2$

$২২। x^{3}y-x{y}^3, (x-y{)}^2$

$২৩।x^2+7x+12 , x^2+9x+20$

$২৪। a^3-a{b}^2 , a^4+2a^{3}b+a^2*b^2$

$২৫। a^2-16 , 3a+12a^2+5a+4$

$২৬। xy-y{x}^{3}y-xy{x}^2-2x+1$

ল.সা.গু. নির্ণয় কর (২৭-৩৬)।

$২৭। 6a^3{b}^{2}c , 9a^{4}b{d}^2$

$২৮।5x^2{y}^{2}10x{z}^3, 15y^3{z}^4$

$২৯। 2p^{2}x{y}^{2}3p{q}^2, 6pq{x}^2$

$৩০। (b^2-c^2)(b+c{)}^2$

$৩১। x^2+2x , x^2+3x+2$

$৩২। 9x^2-25y^2, 15ax-25ay$

$৩৩। x^2-3x-10 , x^2-10x+25$

$৩৪। a^2-7a+12 , a^2+a-20, a^2+2a-15$

$৩৫। x^2-8x+15 , x^2-25 , x^2+2x-15$

$৩৬। x+5 , x^2+5x, x^2+7x+10$

৩৭। a = 2x - 3 এবং b = 2x + 5

(ক) a + b এর মান নির্ণয় কর।
(খ) সূত্রের সাহায্যে $a^2$ এর মান নির্ণয় কর।
(গ) সুত্রের সাহায্যে এ ও b এর গুণফল নির্ণয় কর। x = 2 হলে, ab = কত?

$৩৮। x^2-625$ এবং $x^2+3x-10$ দুটি বীজগণিতীয় রাশি।

(ক) দ্বিতীয় রাশিকে উৎপাদকে বিশ্লেষণ কর।
(খ) রাশি দুটির গ.সা.গু নির্ণয় কর।
(গ) রাশি দুটির ল.সা.গু. নির্ণয় কর।

৩৯। $x^2-3x-10,x^3+6x^2+8x$ এবং $x^4-5x^3-14x^2$ তিনটি বীজগাণিতিক রাশি।

ক) (3x - 2y + z) এর বর্গ নির্ণয় কর।
খ) ১ম ও ২য় রাশির গ.সা.গু নির্ণয় কর।
গ) রাশি তিনটির ল.সা.গু নির্ণয় কর।